How To Determine If A System Has A Nontrivial Solution
How to determine if a system has a nontrivial solution. For your problem adding a 3rd row or not the rank of the matrix is still 2 and there are 3 unknowns so there must be at least one non trivial solution. A solution or example that is not trivial. A 1 a 2 ½.
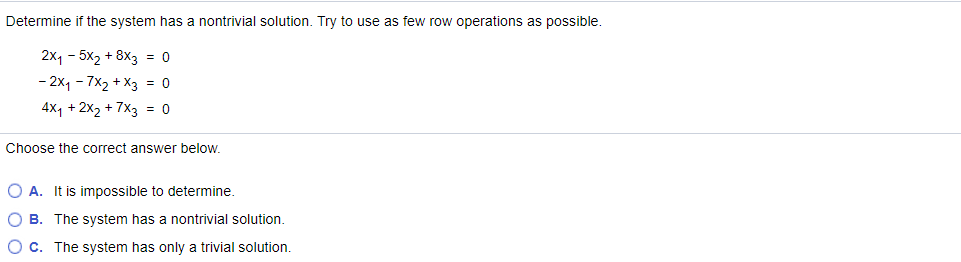
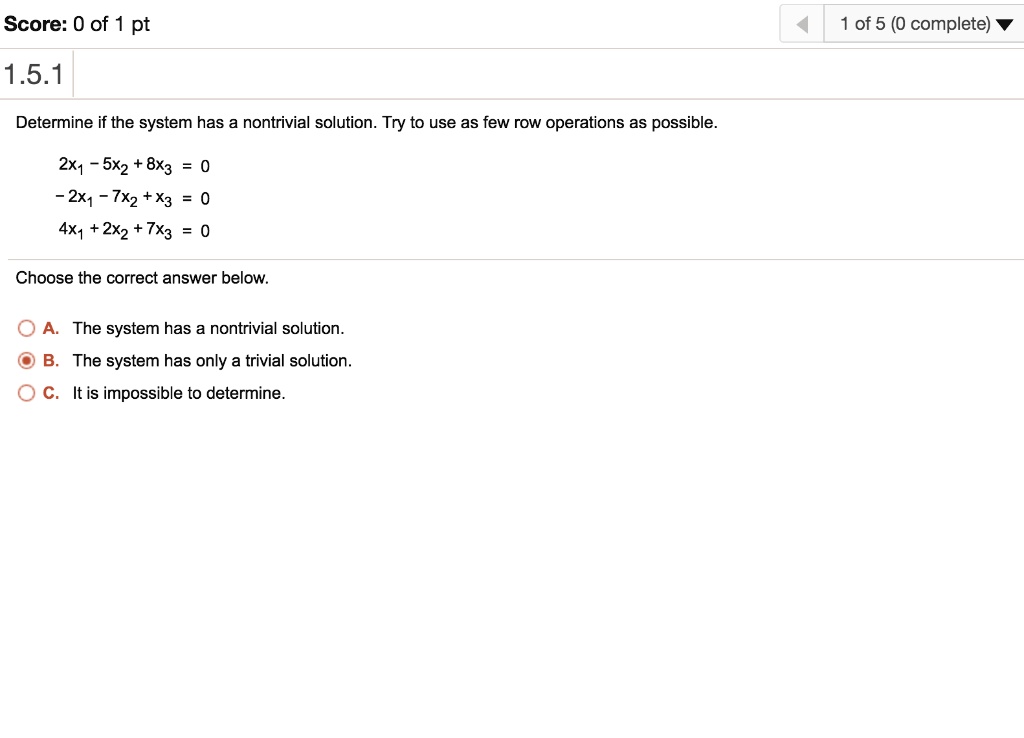
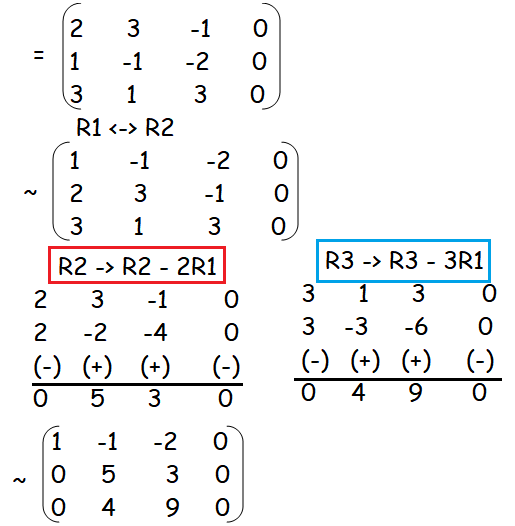
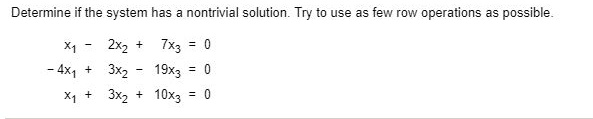
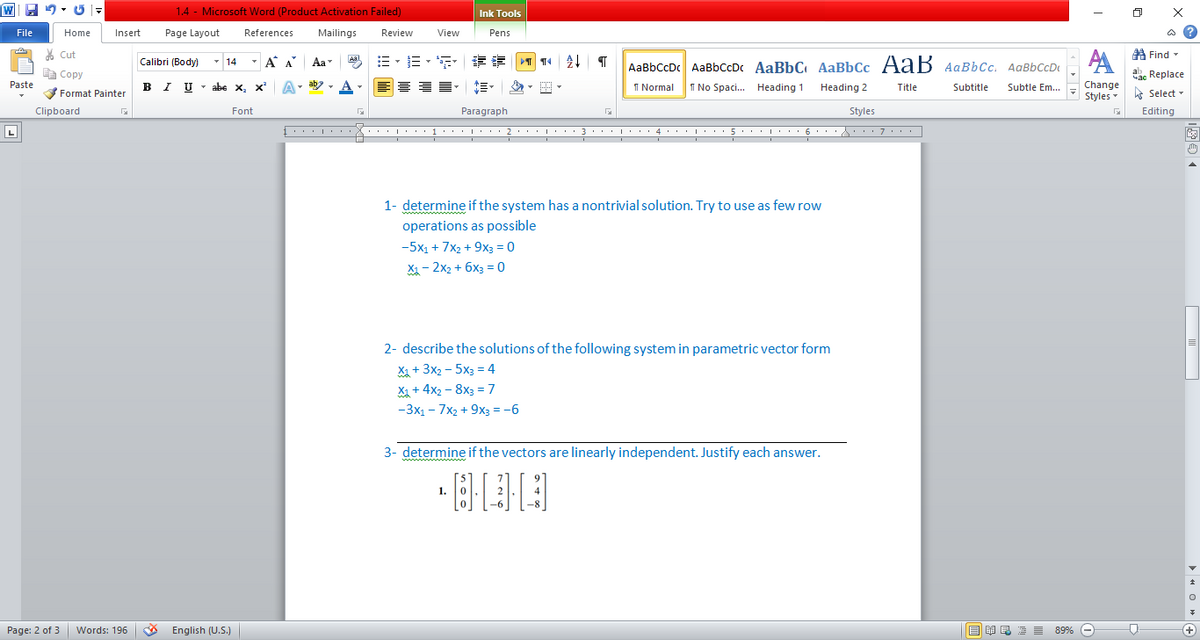
Try to use as few row operations as possible. 2 x 1 5 x 2 8 x 3 0. A homogeneous equation Ax 0 has nontrivial solutions if and only if the system of equations has.
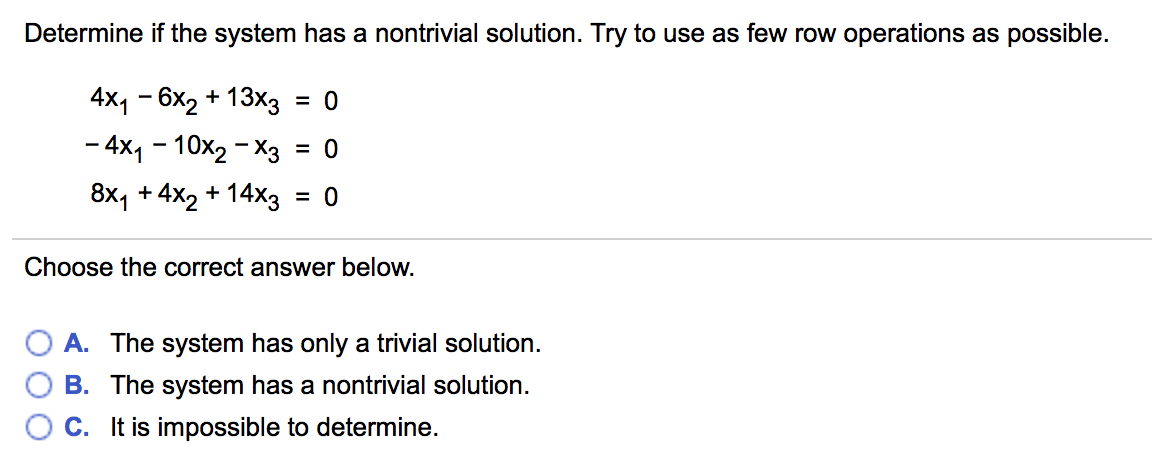
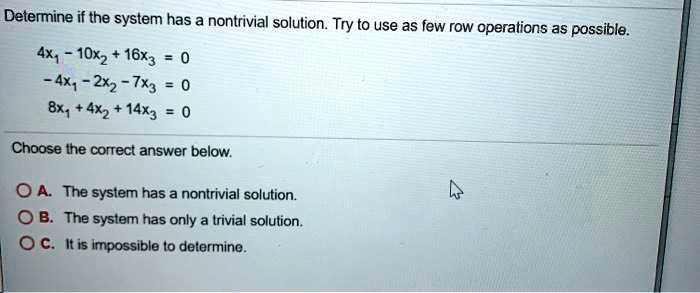
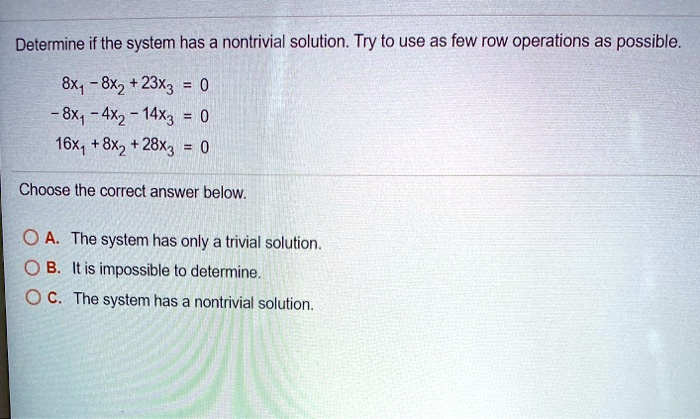
If ρ A ρ A O n then system 2 has a non-trivial solution. Determine If The System Has A Nontrivial Solution. 4x1-6x2 13x3 0 4x1-10x2x3 0 8x14x2 14x3 0 Choose the correct answer below.
Transcribed image text. Topologically nontrivial gapped phases with nonzero Chern. So option B is the answer.
The trivial solution does not tell us much about the system as it says that 00. I a unique solution. A If the system A2x 0 has a nontrivial solution show that Ax 0 also has a nontrivial solution.
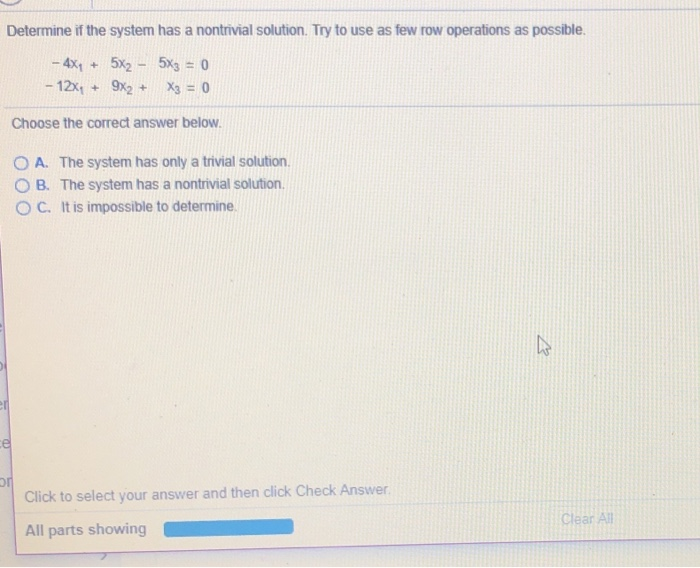
If a homogeneous system of linear equations has more variables than equations then it has a nontrivial solution in fact infinitely many. C 1 c 2 15. Try to use as few row operati.
A 1 a 2 b 1 b 2 c 1 c 2. Nontrivial 0D edge modes of 2D fermion.
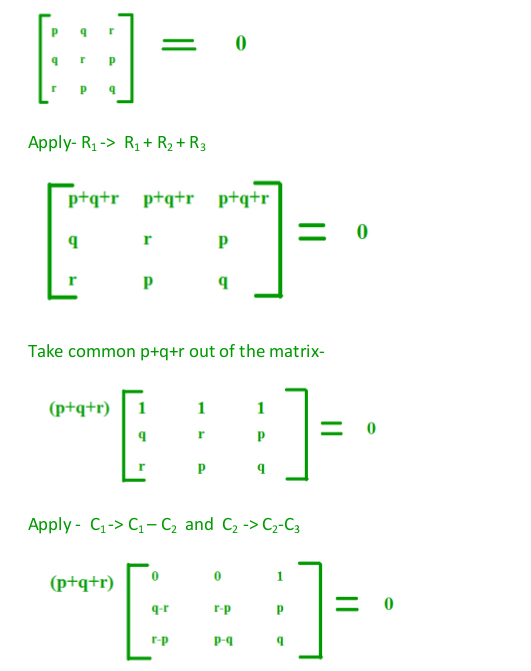
Straight line - Theorem 2.
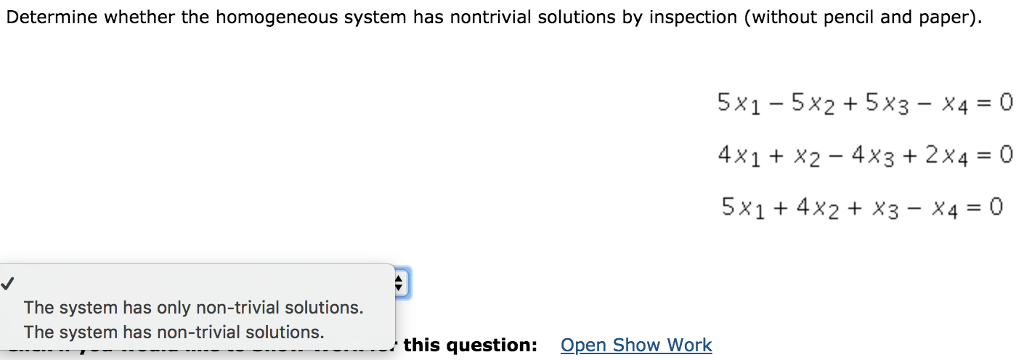
This happens if and only if the system has at least one free variable. The system has only a trivial solution. B Generalize the result of part a to show that if the system Anx 0 has a nontrivial solution for some positive integer n then Ax 0. Topologically nontrivial gapped phases with nonzero Chern. A solution or example that is not trivial. Transcribed image text. A homogeneous system always has a nontrivial solution if the number of equations is less than the number of unknowns. Hence the system of equations has no solution. Ii a non-trivial solution.
The homogeneous system Ax 0 always has the trivial solution x 0. X2y 3 2x4y 15. The systems has trivial solution all the time ie. A 2 2 b 2 4 c 2 -15. 2xı - 5x2 8x3 0 -2xı - 7x2 x3 0 4xı 2x2 7x3 0 x - 3x2 7x3 0 -2x1 x2 - 4x3 0 x1 2x2 9x3 0 3. Often solutions or examples involving the number zero are considered trivial. Thus if the system has a nontrivial solution then it has infinitely many solutions.










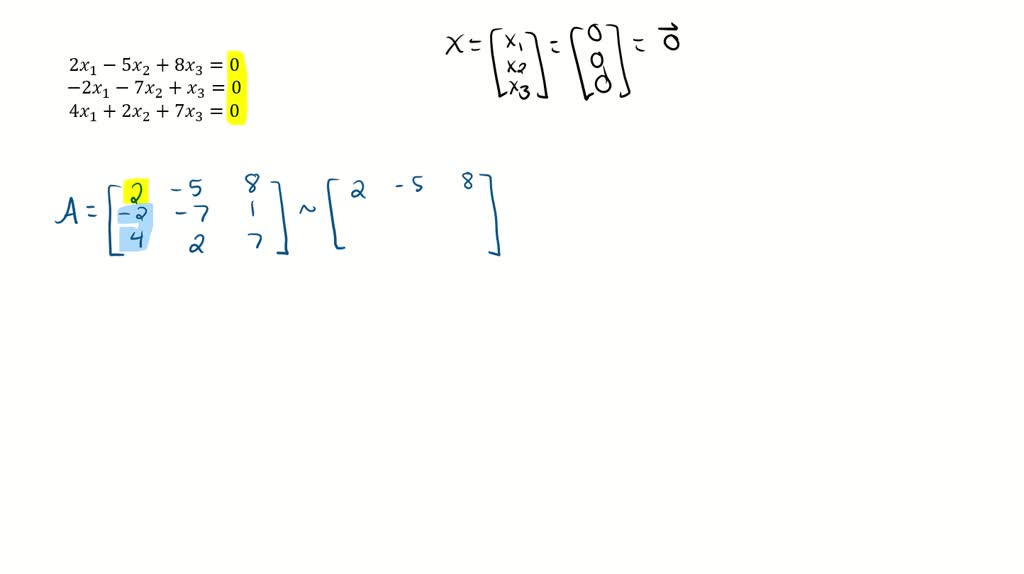








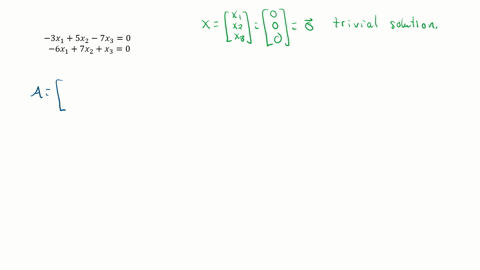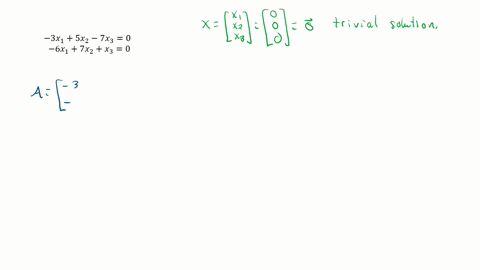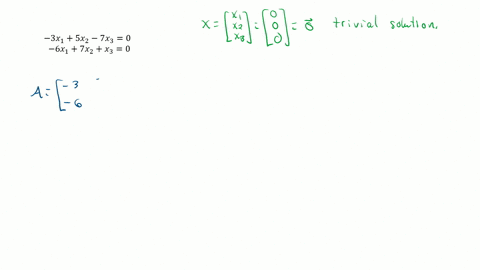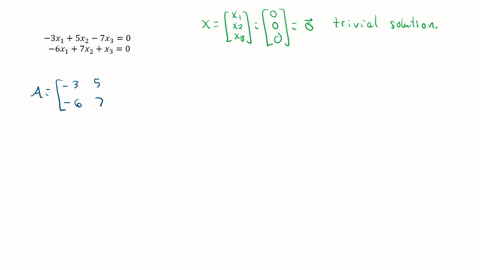










Post a Comment for "How To Determine If A System Has A Nontrivial Solution"